Design and Theory
PWM Waveform Generation
One of the most interesting challenges in building this was to generate PWM from the same chip that is doing everything else. (Most hexapod builds which I have seen use a separate servo controller, which can cost upwards of $30 by itself). This took a lot of work, but I am very happy with the end result.
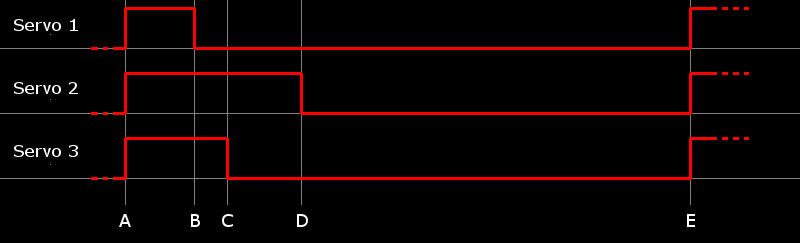
The trick is to use TIMER1, with the two compare resgisters doing different things. COMPA is set once (when you set the period); COMPB is set once per pin. The logic is as follows; we also refer to the timing diagram below which should help visual thinkers (like me) figure out what is happening:
- Initialize the library, specifying the period (20000uS in the case of hobby servos) and the pin / port mappings for each PWM output
- Set various phases for each pin. Every time you set this, the library will re-cacluate the list of pins, in sorted order, along with supporting information
- The PWM waveform begins when COMPA fires (i.e. just after the prevous waveform has completed). In the COMPA ISR, we set all PWM pins high. We then pick the shortest (non-zero) one, and set the COMPB register to fire after this many microseconds. In the diagram, this happens at points A and E.
- When COMPB ISR fires for the first pin (point B in the diagram), we set that pin low, and look up the next lowest pin. We then set COMPB for that pin (point C in the diagram).
- COMPB ISR fires again when the next time (point C) is reached. Repeat these last few steps until all pins have been set low (Point C, D). After the last one, set COMPB to 0xFFFF (i.e. don't fire again)
- COMPA ISR will fire again next, when the end of the period is reached (point E). We are now back at step 3. Repeat.
For more information, and to use / adapt this library for yourself, please browse the Stubby git repo (or check out the entire repo: 'git clone http://git.digitalcave.ca/projects.git', and browse to the directory /lib/avr/pwm).
Leg Design
Stubby differs from other hexapod builds in that the legs are not driven directly by the servos. I am using cheap, low torque servos, which are not able to lift the weight of the robot by themselves. To allow them to work, I use principles of leverage / mechanical advantage to trade movement distance for torque. This limits the range of motion which the legs can move in, but it allows the legs to lift the robot.
Inverse Kinematics
Inverse Kinematics is a big word for a simple concept. "Kinematics" refers to modelling the position of something (in this case, a robot's leg) when angles and leg segment lengths are known. This can be done with simple trigonometry. Inverse kinematics is the opposite: if you want a robot leg to move to point X,Y,Z in 3 dimensional space, and the leg has known segment lengths, what angles should the joints be set to in order to reach this position? It turns out that we can use trigonometry as well.
We make some assumptions here. First, we assume that all calculations are made for the leg with mounting angle 0 (i.e. the middle right leg, if you are viewing from the top). We use linear algebra to rotate the other legs to this position before operating on them. Second, we also assume that the coxa axle is at X,Y position 0,0. We accomplish this by translating the rotated leg by LEG_OFFSET (in my case, 45mm). Also, keep in mind that inverse kinematics starts with a desired point in X,Y,Z co-ordinate space.
This document does not include any actual formulas. To follow along and see the actual math, look at Leg.cpp in the function "Leg::setPosition(Point p)". There are comments which say essentially the same thing as you see on this page, and reference the same diagrams.
The first step is to determine what the desired coxa angle is. This can be done using the atan2() trig function. This function will give you an angle (in radians) when given a point on the X,Y plane. See figure 1 for a visualization of this:
Figure 1:
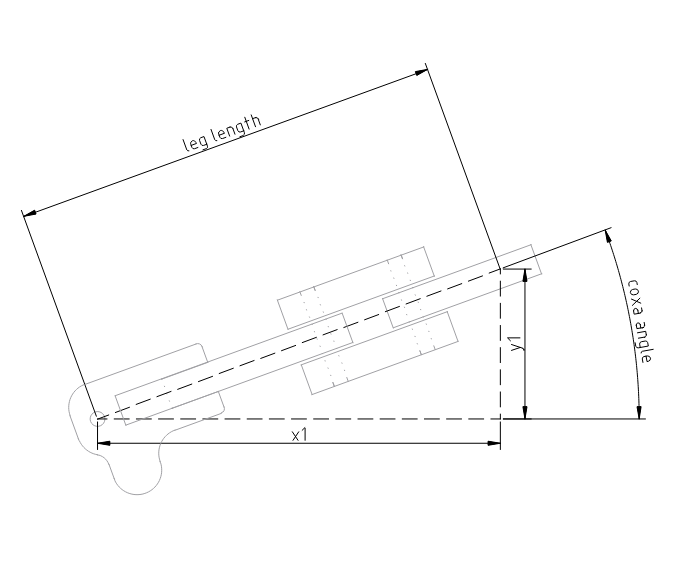
We also need to calculate how far the leg needs to extend. This is the leg length, and is calculated using the Pythagorean theorem (see figure 1).
Next, we need to calculate the desired femur angle. Due to Stubby's frame, this needs to be done in two parts (figure 2 and 3).
Figure 2:
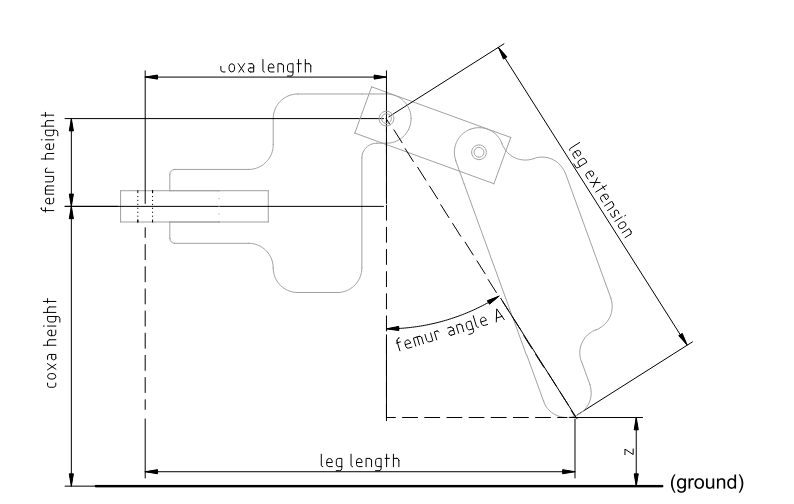
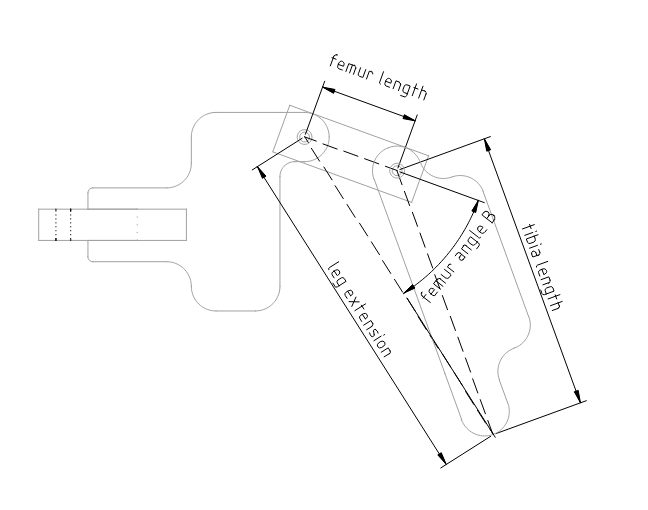
Figure 3:
First, we need to find the distance between the femur joint and the end of the tibia. Do this using the right triangle of (femur_height + coxa_height - z), (leg_length - coxa_length). See figure 2, 'leg extension'.
Once we know the leg extension, we can find "Femur angle A" using the Law of Cosines (There are 6 pieces of information about any triangle: three angles and three lengths. If you know any three of these, you can find the rest using different trigonometric functions. In this case, we know the three side lengths: one is leg_extension, one is (coxa_height + femur_height - z), and the last is (leg_length - coxa_length). See figure 2 to visualize what these lengths are.)
We can now find "Femur angle B", using the same approach as the last step. We know leg_extension (from earlier), and femur_length and tibia_length are constants which can be measured against the robot itself with a ruler.
We add Femur angles A and B together to find the actual desired Femur angle.
The Tibia angle uses the same triangle as we used for Femur angle B; we just need to find a different angle. Thus we can use the same formula (still the Law of Cosines), and just re-arrange the sides. See figure 4.
Figure 4:
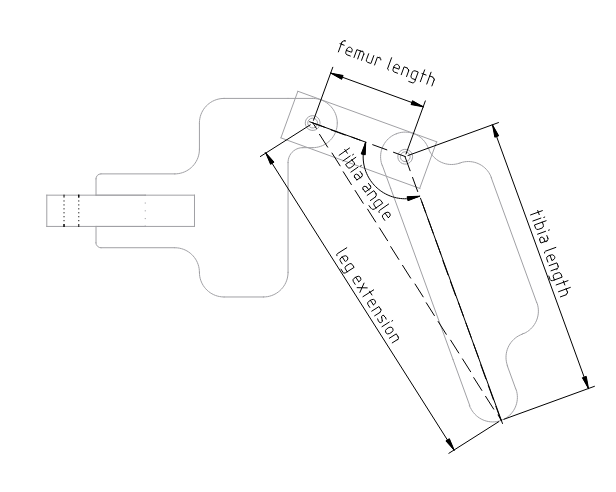
At this point, we are done! We have all three desired angles (coxa, femur, and tibia); by setting the leg to have these angles, we will position the foot at the desired X,Y,Z co-ordinate.